Rachel M. Carmena

Functional programming sparks joy

Published: 5 August 2019
Last updated: 20 September 2019

Motivation

The title comes from Marie Kondo’s recommendation about feeling if an item sparks joy to keep it with you or to discard it.

When I heard about functional programming I decided to continue learning about it. Why? Let’s see some reasons.

Introduction

I agree with Scott Wlaschin when he says that functional programming is not scary but unfamiliar. It has a mathematical basis and is full of new concepts.

However, the more you know about functional programming and working examples, the more advantages you notice in the paradigm.

Which programming language am I going to use for the examples? JavaScript. It’s not a purely functional programming language like Haskell but multi-paradigm, so it’s suitable for talking about it.

Moreover, I think it can be interesting to start practicing with a known and non-purely functional programming language before moving to another one.

Pure functions

One of the objectives is to have pure functions.

A pure function works as follows:

  • It takes an input.
  • It works with that input and no more. It doesn’t access the outside in order to get more things, neither changes it the outside.
  • It returns an output.

This image appears in my mind:

So it has these properties:

  • It returns the same output from the same input.
  • It has no side effects.
  • It’s referentially transparent: a call can be replaced by the output for the present input. It’s not necessary to execute the function to preserve the semantics of the program.

Referential transparency is a simple and powerful concept: Can I replace this function call by its result without altering the program behaviour? Why? Can it be simplified? Would it be necessary to compute that function call every time? Could some results be memoized?

Declarative programming

My Dutch uncle who is now retired and always worked very near developers told me:

I’ve heard that one of the problems in software development is that source code includes a lot of details and we should program at a higher abstraction level.

I think it’s useful to explain this section.

Functional programming is declarative: it doesn’t reveal details of implementation.

For example, imagine that we have the following function:

const isEven = number => (number % 2 === 0);

and we want to know if an array only contains even numbers:

const onlyContainsEvenNumbers = array => {
    for (let index = 0; index < array.length; index++) {
        if (!isEven(array[index])) {
            return false;
        }
    }
    return true;
}

const numbers = [2, 4, 8, 10, 20, 11];
onlyContainsEvenNumbers(numbers); // false

The onlyContainsEvenNumbers function is an example of imperative programming: it includes a lot of details to indicate how to get the goal.

However, compare it with this alternative where an expression is used to describe what to get:

const numbers = [2, 4, 8, 10, 20, 11];
numbers.every(number => isEven(number)); // false

// Following the pointfree style:
numbers.every(isEven); // false

If fewer details are given then: less prone to error and easier to read.

In this case, less tests would be needed because the every function is known to work as expected.

Note: The "point" of pointfree style is not . but a point on a space. f(x) can be read as "the value of f at point x". So pointfree style consists on not specifying the parameters to avoid redundancy.
Note: The function isEven is an example of predicate, a function that returns a boolean value.

Immutability

How many times have you seen a call that modifies the arguments when only an output is expected as a result of that call?

What if the immutability is ensured?

For example, we have a function to calculate the square:

const square = number => Math.pow(number, 2);

and we want to calculate the array of squares from an array of numbers:

const calculateSquares = array => {
    for (let index = 0; index < array.length; index++) {
        array[index] = square(array[index]);
    }
    return array;
}

const numbers = [2, 5, 8];
calculateSquares(numbers); // [4, 25, 64]

Not only a lot of details are given again but also the numbers array is mutated to [4, 25, 64].

However, let’s see the following code:

const numbers = [2, 5, 8];
numbers.map(square); // [4, 25, 64]

In this case, we get the same result and the numbers array remains with the same content at the end.

This is only an example. Immutability is pursued beyond arguments.

The consequences of immutability are testable and parallelizable code.

Note: The map function doesn't only return an array with the same type of items. It accepts a function from the original type to any type.
Note: Moore's law established that the number of transistors on integrated circuits would double every two years. However, the limit was reached for the year 2002. Later, multicore processors appeared to keep the speed increases. Parallelizable code is the only way to take advantage of them.

On the other hand, we can find impure functions in JavaScript like sort:

> const numbers = [100, 1, 8, 25]; 
undefined
> numbers.sort()
[ 1, 100, 25, 8 ]
> numbers
[ 1, 100, 25, 8 ]
> numbers.sort((a, b) => (a - b))
[ 1, 8, 25, 100 ]
> numbers
[ 1, 8, 25, 100 ]

The numbers array is mutated.

That impure function could be wrapped into a pure function:

const sortArray = (array, compareFunction) => {
    const arrayCopy = array.slice();
    return arrayCopy.sort(compareFunction); 
}

> const numbers = [100, 1, 8, 25];
undefined
> sortArray(numbers, (a, b) => (a - b));
[ 1, 8, 25, 100 ]
> numbers
[100, 1, 8, 25]

In production code, I would think about these questions: Where do I need to sort an array? Do I have a lot of functions with an array as a parameter? Should I have to create a new data type?

Note: However, programs usually change the outside world. In that case, what if mutations are isolated in a specific part of the source code?

Higher-order functions

In JavaScript, a function is a first-class citizen:

  • It can be the argument to another function.
  • It can be the output of another function.

A higher-order function is a function that takes another function as an argument or returns another function (or both).

I included examples of every and map so far. Let’s see examples with filter and reduce:

const isEven = number => (number % 2 === 0);

const numbers = [4, 2, 11, 20, 7];
numbers.filter(isEven); // [4, 2, 20]

const add = (accum, value) => accum + value;

const numbers = [4, 10, 1, -10];
numbers.reduce(add); // 5

// Good habit: indicating an initial value
numbers.reduce(add, 0); // 5

The power of having functions as first-class citizens and creating higher-order functions promotes the separation of responsibilities and readability.

Note: When reduce doesn't include an initial value (second parameter), the first item from the array is used as the initial value for the accumulator and skipped. In the included example, it's not necessary to indicate an initial value, because the first item can be used as the initial value and skipped. However, I talked about a good habit to avoid problems with empty lists.
Note: Some programming languages differentiate between reduce (without providing an initial value) and fold (providing an initial value). Others have just fold for both options.

Function composition

Functions can be composed into a new one.

When following the definition of composing two functions, the functions appear from right to left because the output of the first function is the input of the following one.

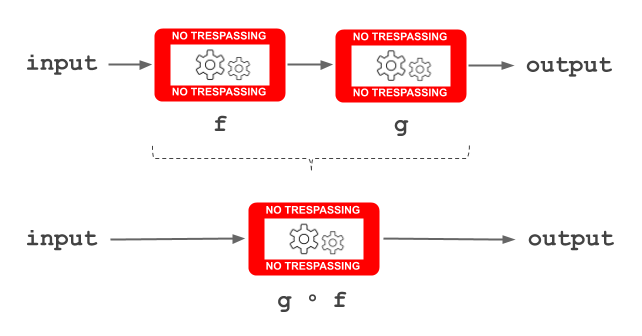
For example, the sumOfSquares function:

const square = array => array.map(number => Math.pow(number, 2));
const sum = array => array.reduce((accum, value) => (accum + value), 0);

const sumOfSquares = numbers => sum(square(numbers));

const numbers = [2, 4];
sumOfSquares(numbers); // 20

However, there are other two ways of composing functions where the functions appear from left to right: pipe or chain.

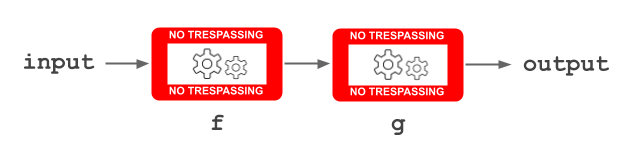
For example, let’s see the sumOfSquares function as a pipe:

const square = array => array.map(number => Math.pow(number, 2));
const sum = array => array.reduce((accum, value) => (accum + value), 0);
const pipe = (f, g) => (...args) => g(f(...args));

const sumOfSquares = numbers => pipe(square, sum)(numbers);

// Following the pointfree style:
const sumOfSquares = pipe(square, sum);

or as a chain:

const square = number => Math.pow(number, 2);
const sum = (accum, value) => (accum + value);

const sumOfSquares = numbers => numbers.map(square)
                                       .reduce(sum, 0);
Note: I only included examples of composing two functions for simplicity though there is no limit.

Tail recursive functions

In functional programming, iteration is usually programmed with recursion so it’s important to control the growth of the call stack.

How? Reusing the call frame instead of adding a new one.

It’s known as tail call optimization or proper tail calls.

Given a recursive function, that optimization is possible if it calls itself as its last action. That is, it’s a tail recursive function.

Let’s see a non-tail recursive function:

const factorial = number =>
    number === 0
        ? 1
        : number * factorial(number - 1);

The stack trace for factorial(4):

factorial(4)
4 * factorial(3)
4 * (3 * factorial(2))
4 * (3 * (2 * factorial(1)))
4 * (3 * (2 * (1 * factorial(0))))
4 * (3 * (2 * (1 * 1)))
4 * (3 * (2 * 1))
4 * (3 * 2)
4 * 6
24

On the other hand, the same function as a tail recursive function:

const factorial = (number, accumulator = 1) =>
    number === 0
        ? accumulator
        : factorial(number - 1, accumulator * number);

The stack trace for factorial(4):

factorial(4)
factorial(3, 4)
factorial(2, 12)
factorial(1, 24)
factorial(0, 24)
24

That’s the reason why it’s possible to reuse the call frame: there is no need to remember the previous calls.

However, the last factorial function could be called with an argument for the accumulator parameter from the beginning:

const WRONG_ARGUMENT = 5;

factorial(4, WRONG_ARGUMENT); // 120

So let’s prevent that error and create an alternative with only one parameter and a closure:

const factorial = number => {
    const fact = (number, accumulator = 1) =>
        number === 0
            ? accumulator
            : fact(number - 1, accumulator * number);
    return fact(number);
}

Currying

Currying consists of converting a function with several parameters into nested unary functions (unary = one parameter).

For example, we have this function with two parameters:

const log = (level, message) => `[${level}] ${message}`;

log("ERROR", "Undefined variable"); // "[ERROR] Undefined variable"
log("INFO", "New post created");    // "[INFO] New post created"

It could be transformed into two nested functions:

const log = level => message => `[${level}] ${message}`;

const logError = log("ERROR");
const logInfo = log("INFO");

logError("Undefined variable"); // "[ERROR] Undefined variable"
logInfo("New post created");    // "[INFO] New post created"

Notice the improvement in readability: logError, logInfo.

Moreover, the need of writing "ERROR" and "INFO" every single time disappears.

I tried to write my own curry function to convert any function into those nested unary functions automatically. The original function can only be called when having all the arguments, so I needed to accumulate the arguments recursively (arity = number of arguments expected by a function):

const curry = fn => {
    const arity = fn.length;
    const _curry = (...args) => 
        args.length === arity
            ? fn(...args)
            : arg => _curry(...args, arg);
    return _curry();
}

Following the previous example:

const log = (level, message) => `[${level}] ${message}`;

const curriedLog = curry(log);

const logError = curriedLog("ERROR");
const logInfo = curriedLog("INFO");

logError("Undefined variable"); // "[ERROR] Undefined variable"
logInfo("New post created");    // "[INFO] New post created"
Note: My own version doesn't work like the curry function that can be found in libraries such as Lodash or Ramda which add more capabilities.
Note: In languages such as Haskell or F#, all functions are considered curried.

Partial application

Partial application consists of doing a projection: specifying only some arguments in function application, producing another function with the remaining parameters.

For example, let’s play with the partial function from Lodash, using an underscore for the unknown arguments:

var _ = require('lodash');
const { log } = console;

const greet = (name, place, message) =>
    `Hello ${name} from ${place}! ${message}`;

const greetFromWonderland = 
    _.partial(greet, _, "Wonderland", _);

const greetFromWonderlandWithWish =
    _.partial(greetFromWonderland, _, "Have a good day!");

log(greetFromWonderlandWithWish("Mike"));
// Hello Mike from Wonderland! Have a good day!
Note: Beyond the included examples, currying and partial application are useful to be able to compose functions.

Another mindset

Last but not least, all of these things (and many more!) make us to think in a different way:

  • Fewer details. We program at a higher abstraction level.
  • It forces ourselves to separate responsibilities in building blocks and then to combine them.
  • Side effects under control. We are more aware of mutations.
  • I didn’t talk about functional data types but I could say that Primitive Obsession smell can be eradicated with this paradigm.

A new mindset is needed to embrace functional programming.

Vocabulary

Some words which weren’t used here although they can be useful to understand other articles:

  • Domain: Set of possible inputs to a given function.
  • Codomain: Set of possible outputs to a given function (the prefix “co” is used to refer to the opposite).
  • Total function (vs. partial function): It returns a valid output for every possible input. They are just known as functions.
  • Polymorphic function: In functional programming, polymorphism is also known as parametric polymorphism. A polymorphic function operates on values without depending on their type. It’s valid for any type.

Next card

Functional programming sparks joy 2

Further knowledge

Acknowledgments

Special thanks to these old colleagues:

And thanks to:

  • Eduardo Sebastian for his pull request to fix some typos.
  • Christophe Riolo Uusivaara for his valuable feedback about tail call optimization. It’s not only related to recursive functions.

Credit

Image by Anke Sundermeier from Pixabay